Matlab FFT Frequency Axis Reconstruction

Time and time again, I find myself needing to remember how to accurately reconstruct the frequency axis of an FFT in Matlab. This is one of the ways that I have documented as being a pretty close approximation of the frequency axis. This code will also properly compute the magnitude of each frequency component.

The code below uses the signal below as an example:

y=5*sin(10*2*pi*x)+3*sin(22*2*pi*x)+cos(13*2*pi*x)+7;

Now the Code:

	% A simple example of how to reconstruct
	% the frequency components from an FFT
	%% Clean up the workspace
	clear all;
	close all;
	clc;
	%% Create the initial parameters
	Window=5; %Set how long in time to sample + and -
	Fs=100; %Set the sampling frequency
	% Fs should be set atleast 2x max
	% frequency in the signal
	% With the signal below, the max frequency is
	% 22Hz meaning we want to sample atleast at 44Hz
	%% Generate the time domain signals
	x=-Window:1/Fs:Window; %Create the time signal
	y=5*sin(10*2*pi*x)+3*sin(22*2*pi*x)+cos(13*2*pi*x)+7;
	% Plot the time domain signal
	figure(1);
	plot(x,y);
	%% Compute and plot the frequency domain signal
	figure(2);
	% Extract the max frequency that the FFT
	% can compute from the Fs we have specified
	fmax=Fs/2; %Application of Nyquist Theorem
	% Compute the magnitude of the fft of y
	N=441;
	FFTy=fftshift(abs(fft(y,N)));
	% The frequency axis is generated using linspace
	f_axix=linspace(-fmax,fmax,N-1);
	% Plot the FFT using stem
	stem(f_axix,FFTy(2:end)./length(FFTy));

view raw fft_reconstruct.m hosted with ❤ by GitHub

Now the result:


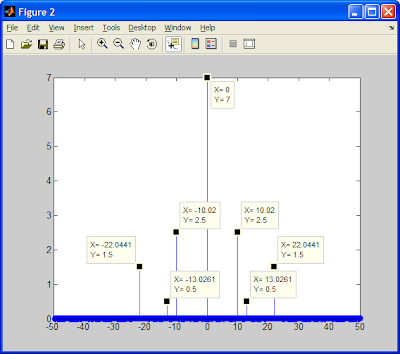
Hope you find this useful.